Комбинаторика (алгоритмы на языке Dart)

Пример простого кода программы для решения задач комбинаторики: перестановки, размещения и сочетания. Второй пример от первого, отличается только разным количеством элементов. Третий от второго, другими начальными значениями циклов.
Поэтому если запомнить один пример, то написать два остальных будет просто. Стоит только немного разобраться в теории и применении комбинаторики.
Данные примеры не являются универсальными для всех задач.

Число перестановок

Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов.

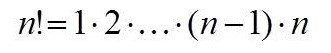
Число перестановок из 3 предметов.

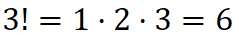
Основные элементы кода программы "Алгоритм перестановки":

• Список list - содержит элементы, которые нужно расставить;
• Три цикла for() - используются для вывода элементов на три места;
  При увеличении мест нужно увеличить количество циклов.
• if () continue - проверка переменных "i, n, m" для использования уникальных элементов;
• num - подсчитывает количество расстановок.

List<int> list = [1, 2, 3];
int num = 0;

for (int i = 0; i < list.length; i++) {
  for (int n = 0; n < list.length; n++) {
    for (int m = 0; m < list.length; m++) {
      if (i == n || i == m || n == m) continue;
      print('${list[i]} , ${list[n]} , ${list[m]}');
      num++;
    }
  }
}

print('num: $num');

Пример вывода в консоль:

1 , 2 , 3
1 , 3 , 2
2 , 1 , 3
2 , 3 , 1
3 , 1 , 2
3 , 2 , 1
num: 6

Число расстановок (Размещения)

Размещениями из n элементов по m называются соединения, которые можно образовать из n элементов, собирая в каждое соединение по m элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.

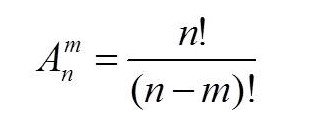
Число расстановок из 6 предметов на 3 места.

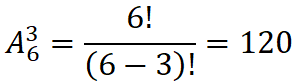
Следующий код отличается от предыдущего только новым списком list, в нем больше элементов.

List<int> list = [1, 2, 3, 4, 5, 6];
int num = 0;

for(int i = 0; i < list.length; i++) {
  for(int n = 0; n < list.length; n++) {
    for(int m = 0; m < list.length; m++) {
      if (i == n || i == m || n == m) continue;
      print('${list[i]} , ${list[n]} , ${list[m]}');
      num++;
    }
  }
}

print('num: $num');

Пример вывода в консоль (большая часть строк пропущена):

1 , 2 , 3
1 , 2 , 4
1 , 2 , 5
..............
6 , 5 , 3
6 , 5 , 4
num: 120

Число сочетаний

Сочетаниями из n элементов по m называются соединения, которые можно образовать из n элементов, собирая в каждое соединение m элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).

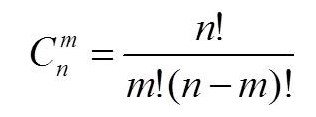
Число сочетаний из 6 предметов по 3.

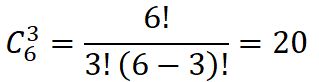
Код для сочетаний отличается от кода расстановок новыми начальными значениями для 2-го и 3-го цикла for.

List<int> list = [1, 2, 3, 4, 5, 6];
int num = 0;

for(int i = 0; i < list.length; i++) {
  for(int n = i; n < list.length; n++) {
    for(int m = n; m < list.length; m++) {
      if (i == n || i == m || n == m) continue;
      print('${list[i]} , ${list[n]} , ${list[m]}');
      num++;
    }
  }
}

print('num: $num');

Пример вывода в консоль

1 , 2 , 3
1 , 2 , 4
1 , 2 , 5
1 , 2 , 6
1 , 3 , 4
1 , 3 , 5
1 , 3 , 6
1 , 4 , 5
1 , 4 , 6
1 , 5 , 6
2 , 3 , 4
2 , 3 , 5
2 , 3 , 6
2 , 4 , 5
2 , 4 , 6
2 , 5 , 6
3 , 4 , 5
3 , 4 , 6
3 , 5 , 6
4 , 5 , 6
num: 20

Подборка заметок

• Создание казуальной 2D игры. Пошаговая инструкция при помощи Flame и Flutter (часть 1 из 5)
• Flutter 2.2: что нового?